在数学分析的发展历史上，数学家们一直猜测：连续函数在其定义区间中，至多除去可列个点外都是可导的。也就是说，连续函数的不可导点至多是可列集。

一、可导的误区

在当时，由于函数的表示手段有限，而仅仅从初等函数或从分段初等函数表示的角度出发去考虑，这个猜想是正确的。但是随着级数理论的发展，函数表示的手段扩展了，数学家可以通过函数项级数来表示更广泛的函数类。

二、处处连续处处不可导函数

Weierstrass是一位研究级数理论的大师，他于1872年利用函数项级数继波尔察诺之后构造出了一个处处连续而处处不可导的函数，为上述猜测做了一个否定的终结（公式如下）

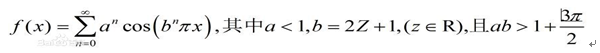
Weierstrass的反例构造出来后，在数学界引起极大的震动，因为对于这类函数，传统的数学方法已无能为力，这使得经典数学陷入又一次危机。但是反过来危机的产生又促使数学家们去思索新的方法对这类函数进行研究，从而促成了一门新的学科“分形几何”的产生。所谓“分形”，就是指几何上的一种“形”，它的局部与整体按某种方式具有相似性。“形”的这种性质又称为“自相似性”。

三、理论的运用

我们知道，经典几何学研究的对象是规则而光滑的几何图形，但是自然界存在着许多不规则不光滑的几何图形，它们都具有上面所述的“自相似性”。如云彩的边界；山峰的轮廓；奇形怪状的海岸线；蜿蜒曲折的河流；材料的无规则裂缝，等等。这些变化无穷的曲线，虽然处处连续，但可能处处不可导。因此“分形几何”自产生起，就得到了数学家们普遍的关注，很快就发展为一门有着广泛应用前景的新的学科。

（基础教学部   宋晓辉  供稿）